热文聚焦

热文聚焦

热文聚焦推荐

张志强｜公司破产风险的定量模型及其应用

发布日期:2022-08-18浏览次数:431标签:振兴会计师事务所,上市公司审计和咨询服务

【摘要】基于破产成本的最新研究突破，通过概念变换和逻辑推导，建立了破产风险计量模型，即破产概率模型和破产损失模型。这两个模型揭示了破产风险的客观逻辑和内在机理。以三家上市公司为例，进一步探讨了模型的应用，即分别评估了三家公司的流量破产风险和存量破产风险。应用探讨证明，模型既适用于危机公司也适用于健康公司。

【关键词】破产风险；破产概率；破产成本；流量破产；存量破产

一、引言

按照常规的理解，公司破产是指公司不能清偿到期债务。在宣告破产的情况下，公司无力继续经营，或者不得不终止经营，对公司财产进行破产清算，清算所得用于补偿公司债权人。公司破产风险通常就指发生上述情况的可能性。

无论是破产还是破产风险，人们往往都试图规避。由此出现了各种替代词汇，比如，破产（bankruptcy）改称违约（default），破产风险（bankruptcyrisk）改称违约风险（defaultrisk）、信用风险（creditrisk）、无力清偿风险（insolvencyrisk）、财务困境（financialdistress）、财务失败（financialfailure）等。然而，这并不利于避免或摆脱破产，也不利于对破产风险的事先计量与事后应对。

就常规的公司而言，每年发生破产的概率往往很小。然而，这并不意味着破产风险就不存在，更不意味着破产风险的研究不重要。相反，破产风险的研究非常重要，因为无论破产或类似的表达多么不受欢迎，公司最终都难免走向破产或消失；在此之前，公司必须时时提防和考虑破产风险。另外，资本市场上有关各方（如银行、分析师等）难免要从破产风险这个角度评判公司，既包括有破产危险的公司，也包括正常或健康的公司。

破产风险其实只是公司面临的风险之一。简单划分，公司风险可分为经营风险与财务风险两大类。信用风险、违约风险、破产风险都是指公司不能如期足额归还债务本息的风险，只是不同场合的表达习惯或目的不同，本质上没有多大区别。

破产分为流量破产和存量破产两种情况。流量破产指公司的现金流量不足以偿还到期债务；存量破产指资不抵债，即公司价值低于债务价值，通过变卖资产也不能全额偿还债务。一般而言，两种破产的后续处理不同：存量破产需要公司变卖资产来偿还到期债务，即破产清算，其结果往往是不能保全债权人的利益，留给公司股东的财产所剩无几；流量破产往往通过债务和资产重组帮助公司渡过难关，同时最大限度地保护债权人利益。因此，在破产无法避免的情况下，有关各方往往会尽可能争取流量破产，避免存量破产。

本文专注于研究破产风险的计量，主要创新是基于严谨的概念和逻辑推导构建了破产风险计量模型，并进一步将该模型应用于流量破产和存量破产风险的计量。基于本文的创新模型，还可以厘清现实中常见的财务比率（如流动比率、负债率等）与公司破产概率的定量关系。

二、相关研究综述

现实中，有关公司破产风险的研究主要分布在三个领域：一是财报分析中的偿债能力研究，主要是通过有关比率的计算来判断公司的偿债能力，进而确定破产风险；二是财务预警的研究，主要是应用统计分析得出影响公司破产的重要因素，从而确定公司破产风险；三是近年来较为盛行的公司财务造假的研究，主要是通过个案的研究确定具体公司财务数据的真实性。其实，关于破产风险的研究，需要回答一个简单的问题，即公司的破产概率为多大？也可以进一步细分为流量破产、存量破产的概率，以及短期和长期的破产概率等。上述三个领域的破产风险研究都很有价值，美中不足的是，都不能回答破产概率的问题。

1.偿债能力的研究。有关偿债能力的研究侧重于计算和分析财务比率，具体包括：反映短期偿债能力的流动比率和速动比率，反映长期偿债能力的资产负债率、利息保障倍数等。现实中还有权益乘数、产权比率等指标，其实是资产负债率的变形，不提供增量信息。具体计算公式如下：

可以说，这些比率通常可以在一定程度上反映公司的偿债能力；而偿债能力越强，则破产可能性越小。因此，可以依据这些比率评判公司的破产风险。可惜的是，这些比率与破产风险和破产概率的关系模糊不清。比如，某公司利息保障倍数为3倍，代表破产风险是高还是低，或者是多高的破产风险？再比如，正常情况下，流动比率不能小于1，即公司每1元当年需要归还的负债，必须至少有1元当年可以变现的资产作为保障。这也是迄今为止这些比率中唯一有明确“理论标准”的比率。可是，如果一家公司的流动比率等于1或1.2，其破产概率为多大呢？

这是很容易就会想到的问题，也是关注破产风险研究的相关各方迫切想知道答案的基本问题。但有关偿债能力的研究无法给出答案，财务理论和实务中目前也没有解答的方法或模型①。当然，复杂一点的问题就更难以解答了。比如，两家公司A和B，假设用公司价值波动率（σ）代表风险，A的波动率和流动比率分别是20%和1.2，B分别是30%和1.8，哪家公司的破产风险更大呢？类似地，A的波动率和负债率分别是20%和60%，B分别是30%和40%，哪家公司的破产风险更大呢？

由此可见，通过财务比率分析公司的偿债能力和破产风险有其道理，但似乎过于简单化了。值得指出的是，这类研究不能揭示有关比率与破产或破产风险之间的确切关系。

2.财务预警的研究。有关财务预警的研究主要是应用统计方法分析公司财务数据，试图预测公司是否会破产，可以说是对简单的财务比率分析的某种延伸或拓展。

早在1932年，Fitzpatrick就利用财务比率进行破产预测，发现最有效的是“净利润/股东权益”和“股东权益/负债”两个比率。Beaver等针对30个财务比率进行破产预测研究，发现三个比率特别有效，即债务保障率（现金流量/债务总额）、资产收益率（净收益/资产总额）、资产负债率（债务总额/资产总额）。这些开创性研究具有简单易行、操作性强的优势，但局限性也较为明显。所选的财务比率往往不能全面反映公司情况，特别容易受财务报表粉饰的影响。20世纪60年代，出现了一些较有影响的研究，如Z计分模型等。

1968年，纽约大学Stern商学院EdwardAltman教授对比破产公司与正常公司，采用多变量统计方法，从财务比率中选出5个最具预测能力的比率，即营运资金/资产总额（X1）、留存收益/资产总额（X2）、息税前利润/资产总额（X3）、股份市值/负债账面价值总额（X4）、销售收入/资产总额（X5），并将其加权平均值称为Z值。Z值越小，表明企业越可能发生破产危险；Z≥2.68和Z≤1.81，分别代表发生破产危险很小和很大的情况。1977年Edward又对模型进行了修正和改进，提出了ZETA模型。

此后破产风险的研究进一步从统计方法中挖掘建立模型的潜力，一个突出表现是Logistic回归模型的广泛应用。该类模型是医学中最常用的模型，能够克服线性方程受统计假设约束的局限性，具有更广泛的适用范围。

20世纪80年代以来，工程领域兴起了人工神经网络（ArtificialNeuralNetwork）以及机器学习（MachineLearning，ML）的研究和应用。它避免了模型形式、变量及其分布特征选择的难题，同时对样本没有限制，还具有较高的并行计算能力、自学能力和容错能力。虽然在破产风险研究中也有尝试借鉴，但似乎还未见效。

我国学者在统计方法上有较丰富的研究。如吴世农、黄世忠早在1986年就尝试借助偿债能力比率来预测公司破产风险。周守华等在1996年借鉴Altman研究建立了F分数模型。吴世农、卢贤义进行了破产风险研究，发现多变量模型优于单变量模型，且Logistic模型效果最好。上述研究选取的预测变量有盈利增长指数、资产报酬率、流动比率、负债股东权益比率、营运资本比率、资产周转率等。宋鹏、张信东也运用Logistic模型针对我国上市公司展开了财务危机预警的研究等。

统计方法的优势是必定能得到结论，劣势是得不到确切结论。因为模型形式、模型变量以及数据的处理方式都是主观选择的，而且不受专业逻辑或破产风险的内在机理约束，这些主观选择的余地似乎为无穷大，或者说不清楚选择的余地有多大，因此统计模型中难免有太多的个人主观因素，过多受个人主观偏好的影响。

事实上，社会科学领域的数据“质量”②远低于自然科学领域。在社会科学领域，根据一套过去数据得出结论的偶然性究竟多大，学术上一直没有深入讨论和研究。需要明确的是，样本数据再大，相比数据整体来说也不过是沧海一粟；更为重要的是，就决策需要而言，应该依据的不是过去的数据，而是未来的数据。跨专业的借鉴值得提倡，但也不能过于盲目和草率；在对问题缺少专业理解的情况下应用非专业方法分析问题，难免主观随意甚至外行。

应用统计方法的研究得不出一致的模型，因为不同的数据会得出不同的模型，包括模型自变量和模型参数都会因样本数据不同而不同；甚至同一套数据也会因处理（如分类）方法的不同以及主观假设的模型形式不同，而导致结论不同。这意味着，随着新数据源源不断产生，新模型也会源源不断出现。从宽泛的意义上讲，科学研究的目的在于解答问题。如果一个问题的解答源源不断，那么这个问题到底是解答了还是没解答呢？

3.财务造假的研究。当前，财务造假研究的升温反映了上市公司的财务造假行为流行的现实。事实上，破产风险评估或计量的结论依赖于两个要素：一个是基础数据，另一个是计算模型。偿债能力研究与财务预警研究的目的都是得出通用或较为通用的计算模型，而财务造假的研究则聚焦于公司数据或信息真实性的问题。

如果说财务预警的研究更多属于统计研究，那么财务造假的研究则更多属于会计研究，因为财务造假即会计数据造假。该类研究的一个优势是：如果公司涉嫌严重财务造假，则可能原因是真实情况不可告人，破产风险很大，破产概率接近100%。对于这种较为极端的情况，不需要模型计算就可以得出结论；该类研究劣势也在于此，即只能针对个案即有问题的公司，不适用于多数公司，特别是不适用于健康公司。而且公司财务造假在原因、手段以及操作方面千差万别，一次甚至多次的研究未必可以得出通用的公式或模型。也就是说，对每家公司的研究都是另起炉灶、从头开始。

披露财务造假旨在纠正会计或财务数据错误，或得到真实数据，而本文重在探讨计算破产概率的方法或模型。对于破产风险的评估而言，数据与模型都很重要，它们之间是互补关系，不能相互替代。因此，财务造假不属于本文研究的重点。

三、研究设计

1.研究目标。公司破产风险计量研究的目的在于得到计算公司破产概率的方法或模型，最好可以分别计算流量破产和存量破产的概率。

2.基础数据。考虑到应用的可行性与便利性，最好以常见的财务数据作为基础数据，比如财务比率分析中的数据，具体包括流动资产、流动负债、总资产、总负债等。根据常规理解，破产风险一方面取决于公司总体的业务风险，另一方面取决于公司的负债情况，这方面的风险也称为财务风险。因此，最终模型或方法所需的数据应该是与公司总体的业务风险以及财务风险相关的常见财务数据。

3.研究方法。考虑到财务预警研究的不足，本文力争避免选取基于不确定的数据得出统计结论的方法。所谓风险的大小，常规做法是从发生概率和潜在损失两个维度进行测算。本文遵循这个常规做法，用专业方法即财务方法评估破产风险③，着重于破产概率和破产成本的测算；其中破产成本即指破产的预期损失。同时，凭借方法上的优势，尝试区分流量破产和存量破产进行探讨。

四、ZZ破产成本模型与破产概率模型

为求解公司最优资本结构，张志强、肖淑芳基于财务理论面向决策的基本特性，修正了对破产成本的长期误解④，分析得出：公司与负债相联系的破产成本实际是该公司价值的卖方期权。这个卖方期权的约定价格为债务的到期价值，到期时间为债务的平均到期时间。在此基础上推导建立了破产成本模型，即：

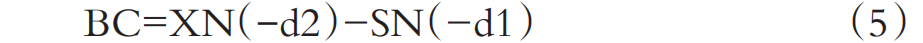
式（5）中，BC为破产成本；S为公司目前价值；X为公司债务的本金，按照研究惯例，它也是债务的现值。N（-d2）和N（-d1）分别为标准正态分布中变量值取-d2和-d1时的累积概率。其中，d1和d2可分别按式（6）、式（7）求得。此处的X与标准期权定价模型Black-Scholes模型中的X略有不同，即X为现值而不是T时间的值。正因为如此，式（5）与标准的卖方期权价值模型略有不同，相应地，d1、d2的表达式也与Black-Scholes模型中的表达式略有不同。

其中：T为公司债务的期限（年），在公司有多笔债务的情况下，可取各笔债务的平均期限；σ为公司价值的波动率，代表公司的风险大小，是财务中最基本的风险指标，常见值范围大致为10%~40%之间。L=X/S，L为公司总资本中的债务比率。根据期权定价基本原理，N（-d2）为该（卖方）期权到期执行的概率，因此也就相当于该公司的破产概率。用大写的P代表这个概率，注意P所代表的是存量破产的概率，即在整个债务期间公司出现因资不抵债而破产的概率。

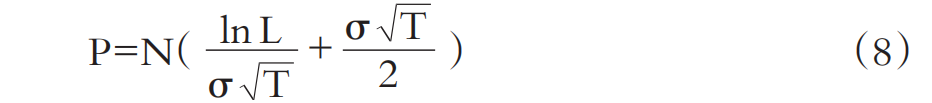
为方便起见，将式（5）和（8）分别称为ZZ破产成本模型和ZZ破产概率模型。破产概率P计量了破产发生的可能性；破产成本BC则计量了破产的潜在损失。

模型中的波动率σ指公司价值的波动率，可以根据公司股权和债权（债务资本）的波动率综合计算得出。公司股权的波动率通常根据过去一段连续时间内股票每日收盘价进行估计。根据股票每日收盘价先计算股票日收益率，然后求出日收益率的标准差，进而年化得到年收益率的标准差，即为公司股票的波动率。债券或债务资本的波动率也可按照类似的方式求得。如果公司没有债券上市，可按照可比公司债券价格计算。最后，依据公司股权资本和债务资本之间收益的相关性，即可基于债务和股权的波动率计算公司总体的波动率σ。

五、流量破产和存量破产的概率

关于存量破产和流量破产，可理解为：流量破产为近期或1年内无法还债的情况；存量破产是指长期无法还债的情况。长期还债靠公司的总资产支持；近期或1年内还债靠公司的流动资产支持。当然，近期或1年内需要还债的数额由公司的流动负债规模决定。因此，对应于公司总资产负债率，可以将公司流动负债占流动资产的比率定义为流动资产负债率。可以理解，流动资产负债率即为流动比率的倒数。

流动资产为公司拥有的一年内可以正常变现的资产；流动负债则为公司在一年内需要归还的债务。还债需要现金，特别是经营获得的现金。为还债而变卖非流动资产（如厂房、机器设备）属于非正常现象。因此可以认为，要确保不发生流量破产，公司应该有足够的流动资产作为保证。传统意义上认为，流动比率最低界限为1，相当于流动资产负债率等于100%。除非公司有高增值且畅销的存货或者有力的外部融资支持，否则流动比率若等于1，债务偿还违约或流量破产是很可能发生的。当然，这种情况下流量破产概率即流动债务违约的概率究竟多大，还没有一个可以信赖的计算方法或模型。

ZZ破产概率和破产成本原本是针对存量破产的计算方法。根据前述分析，短期或流动债务需要依靠正常的流动资产变现来归还。因此，ZZ破产概率和ZZ破产成本自然也可以针对流动资产与流动负债的对比情况（即针对流动资产负债率）来计算，从而用于评估流量破产的风险。

六、案例应用探讨

1.基础数据准备。下面以我国三大家电公司美的、格力和海尔作为案例，做具体的应用探讨。三家公司截至2020年9月30日的有关最新财务数据如表1所示。

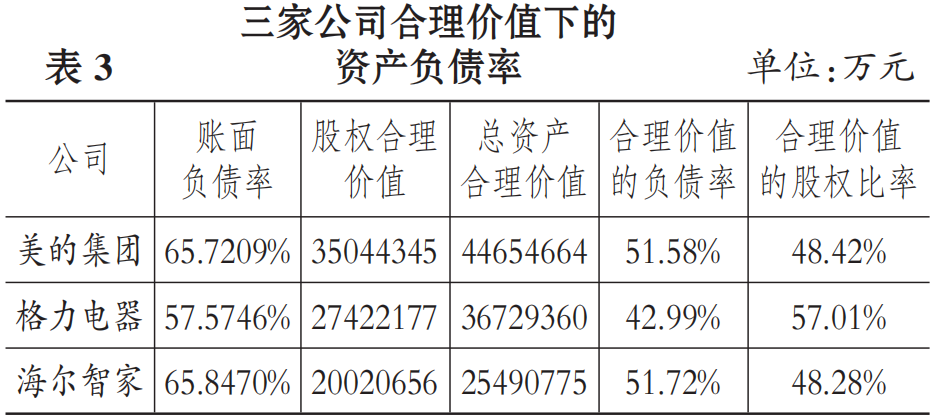
公司股权价值不同于其账面价值，这个差异直接影响公司负债率等有关指标的计算，因为模型中的负债率为合理价值下的负债率。可以认为，公司股权的合理价值等于股权的账面价值乘以合理的市净率。为简化研究，假定三家公司的市净率都为1.8倍⑤。根据表1可计算出公司股权和总资产的合理价值（如表2所示）；进一步可以计算出合理价值下的资产负债率（如表3所示）。

如前所述，可以根据公司股票价格计算股权波动率，再计算债权（债务资本）波动率。如果假定公司股权资本和债务资本收益完全正相关，则加权平均两个波动率就可以得到公司总体的价值波动率。为节省篇幅，下面仅以最新一个月的股价数据演示波动率的计算，债权部分的波动率简单假定为股权波动率的1/4。然后根据表3中合理价值下的负债率、合理价值的股权比率加权平均得到公司总体的波动率。三家公司2021年1月的股价数据如表4所示。基于表4数据，已知三家公司在2020年12月31日股价分别为98.44、61.94、29.21元，则可以计算三家公司在2021年1月每天的收益率，具体如表5所示。

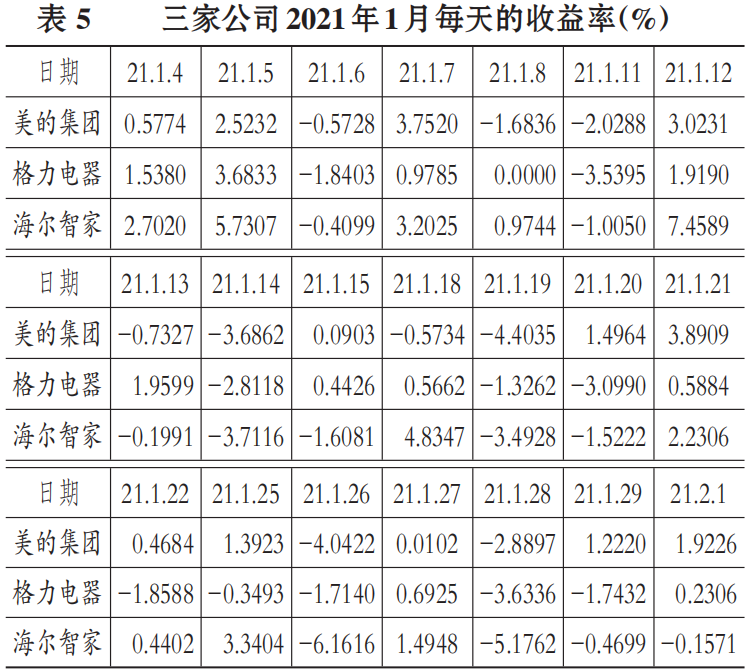
由此，可以用公式或Excel内置函数计算这些收益率的标准差。经计算得出，三家公司日收益率的标准差分别为2.45%、2.00%、3.48%。需要注意的是，因为是每个营业日收益率的标准差，因此应该按照一年的营业天数换算为年标准差。粗略计算，一年有约250个营业日。这些日收益率标准差分别乘以250的平方根，即得到年化的标准差，即股权波动率。计算得出，三家公司分别为38.80%、31.55%、55.07%。进一步假设债务资本波动率为股权波动率的1/4，根据表3计算的负债率和股权比率即可得出三家公司各自的总波动率，分别为23.79%、21.38%、33.71%。当然，股权资本和债务资本的波动率加权平均得出总波动率，相当于假定公司股权资本和债务资本完全正相关。如果假定两者之间不相关，计算略微复杂一点，得出的总波动率也略小一点。究竟应该按哪种假定计算，可根据实际情况确定。

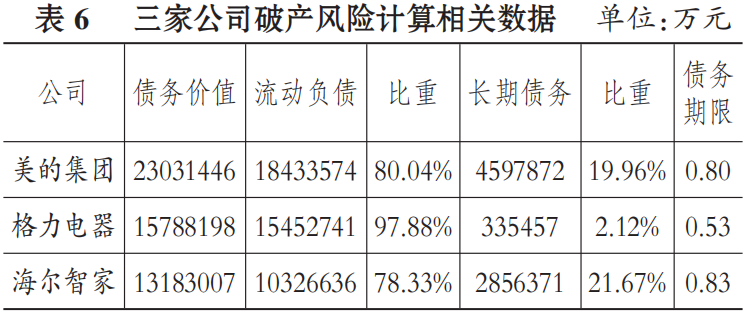
破产风险计算中还需要估计债务平均期限T。假定流动负债平均期限为0.5年，长期债务平均为2年⑥，则三家公司债务平均期限计算如表6所示。

2.破产风险评估。将按照存量破产和流量破产分别评估三家公司的破产风险。

（1）存量破产风险评估。基于模型（5）、（8）以及上述基础数据，可以计算美的、格力和海尔的破产概率与破产成本，结果汇总在表7中。

表7中，N（-d2）列即为破产概率，严格来讲是一个债务周期内的破产概率。可以看出，最低的是格力，其次是美的，海尔略高，但也仅有2%多一点。这基本反映了这三家家电巨头的实际情况。从破产成本的绝对数来看，三家公司差别更为明显。格力的破产成本可以忽略不计，而美的和海尔分别为1700多万和3亿。虽然数字不小，但与公司整体的体量相比，还是微不足道。

显然，运用ZZ破产概率模型和破产成本模型，可以方便地计算和评判健康公司的破产风险。可以说，这三家公司，凭直觉和常规方法判断可能没有多大差别，但通过模型计算却可以明察秋毫。这两个模型的计算结果甚至比评级公司的判断更为精细、清晰。可以想象，如果让评级公司来评级，这三家公司很可能同属一个风险级别，比如都是AAA级。这一点尤其重要，如果公司已经资不抵债，再计算其破产概率等，可能为时已晚。因此，银行对于客户或潜在客户的风险评估，可以采用ZZ破产概率模型和破产成本模型，对所有客户进行测算，进而排序、筛选等。

（2）流量破产风险评估。经过与计算存量破产类似的过程，可以得出三家公司的流量破产概率与破产成本，结果汇总在表8中。

可以看出，三家公司的流量破产风险都明显高于存量破产风险。这是因为三家公司的流动资产负债率都明显高于总资产负债率。海尔的流动资产负债率更高，达到92.58%，因此海尔的流动资产破产概率也高，超过40%。也就是说，若依靠流动资产变现归还流动负债，则出现拖欠的概率约为41.91%。对于债权人而言，不必过于担心，因为流量破产概率超过40%，在存量破产概率不高的情况下，最多会发生拖欠，一般不会有更严重的情况发生。从海尔来看，则应该引起重视，因为反常的拖欠会有损公司声誉，而且可能增加管理工作量以及引起其他不必要的麻烦。因此，海尔应该更加关注有关现金的流入和流出，必要的话可以进一步增加短期融资。

可见，类似海尔这样的绩优蓝筹股破产概率都不是零，而且流量破产概率也不低，这充分说明破产风险需要公司时刻关注。上述计算结果也说明，ZZ破产概率模型对公司的财务情况高度灵敏，可以充分展示公司间破产风险的差异。

当公司的流动比率接近于1或更低时，按照ZZ破产概率模型计算出的流量破产概率会迅速上升。以上述三家公司平均的期间波动率18.59%为标准，计算流动比率在0.5~2.0之间时公司的流量破产概率，具体如表9所示。

需要注意的是，表9中负债率指流动资产负债率，N（-d2）指流量破产概率。可见，在流动比率超过1的情况下，随着流动比率的增大，发生流量破产的概率迅速下降，从50%左右下降到不到1%。但当流动比率小于1时，发生流量破产的可能性很大；随着流动比率下降，破产概率迅速上升，从50%左右上升到超过99%。显然，有了计算破产概率的模型，传统的财务比率也有了更丰富更明确的意义，评估和比较公司的破产风险也容易多了。

七、研究结论

基于ZZ破产成本模型，可以评估公司在具体时间的破产风险，即可以计算其破产概率和破产损失。本文研究发现，这样的破产概率模型和破产损失，可以针对短期中公司的流量破产进行计算，也可以针对长期中公司的存量破产进行计算，当然，也可以据此换算出年均破产概率。可见，本文构建的破产风险评估模型具有较强的灵活性与实用性。

本文模型是基于严谨逻辑构建的封闭解模型，基于这些模型可以将人们熟悉的流动比率、资产负债率等财务比率转换为流量和存量破产概率数据，丰富财务比率的评估和决策含义。在风险管理、财报分析以及公司金融的研究中，人们早就对流动比率、资产负债率、利息保障倍数与破产概率的关系感兴趣，但要得到确切的数量关系却极其困难。本文借助ZZ破产成本模型解决了这样的定量难题，即得出ZZ破产概率模型和破产损失模型。这是本文研究的理论贡献。

基于上市公司的案例分析发现，ZZ破产概率和破产成本模型可以灵敏地反映公司总体风险和负债率等因素的变化，得出相应的破产概率和破产成本，该模型是计量和评估公司破产风险的有效工具。同时，所有公司短期和长期的破产概率都大于零，无论目前多么健康的公司，其存量和流量破产概率都不可能等于零。作为公司收益与价值波动的“底线”，破产风险其实并非只与少数“不健康”的公司有关，包括健康公司在内的所有公司都应该保持对破产风险的高度关注。外部股权（股票）或债权（债券）投资者则更需要运用类似ZZ破产概率和破产成本模型这样的工具来计量和评判所有潜在投资对象的破产风险。

注释

①应该明确，这里的模型指正规的模型，即基于严格逻辑推导得出的模型，而不是人为规定或猜测的模型。只有基于严格逻辑推导得出了模型，才可能代表问题得到解决或解答。否则，如果人为规定和猜测的模型也算解决问题，世界上就没有什么难题了。果真如此的话，期权定价问题早在17世纪30年代郁金香泡沫时期就解决了，用不着等到1973年。因为郁金香泡沫时期就有大量的期权交易数据，可以猜测模型形式和变量并基于市场数据回归得出模型。当然，正如业内人士都知道的，直到1973年的Black-Scholes模型提出，才有了严格符合概念和逻辑的期权定价模型。

②数据的质量可以理解为数据取值的稳定性，或数据作为现象与本质的一致性或联系的紧密性。

③对风险的计量与测算，包括考虑风险确定贴现率和计算资产价值，是财务或金融学科的特长。

④长期以来，财务领域对破产成本都采取统计方法进行研究。然而，从公司风险管理和资本结构角度看，破产成本都是决策变量。决策要面向未来，统计过去的数据无法解决破产成本的计量问题。

⑤这里只是简单假定，重点在于演示方法和模型的应用，实际中市净率未必是1.8，三家公司也未必相同。

⑥我国上市公司长期负债普遍较少，这三家公司也是如此，而且长期负债期限也较短。

参考文献

［1］Beaver，WilliamH..FinancialRatiosasPredictorsofFailure［J］．JournalofAccountingResearch，1966（4）：71~111．

［2］Beaver，WilliamH..AlternativeAccountingMeasuresasPredictorsofFailure［J］．TheAccountingReview，1968（43）：113~122．

［3］EdwardI.Altman.FinancialRatios，DiscriminantAnalysisandthePredictionofCorporateBankruptcy［J］．JournalofFinance，1968（9）：189~209．

［4］EdwardI.Altman，R.Haldeman，P.Narayanan.ZetaAnalysis：ANewModeltoIdentifyBankruptcyRiskofCorporations［J］．JournalofBanking&Finance，1977（1）：29~53．

［5］Agarwal，Vineet，RichardJ.Taffler.Twenty-FiveYearsoftheTafflerZ-ScoreModel：DoesItReallyHavePredictiveAbility？［J］．AccountingandBusinessResearch，2007（37）：285~300．

［6］Ashraf，Sumaira，ElisabeteG.S.Félix，ZéliaSerrasqueiro.DoTraditionalFinancialDistressPredictionModelsPredicttheEarlyWarningSignsofFinancialDistress？［J］．JournalofRiskandFinancialManagement，2019（12）：55~66．